문제
문제링크: https://www.acmicpc.net/problem/30961
풀이방법
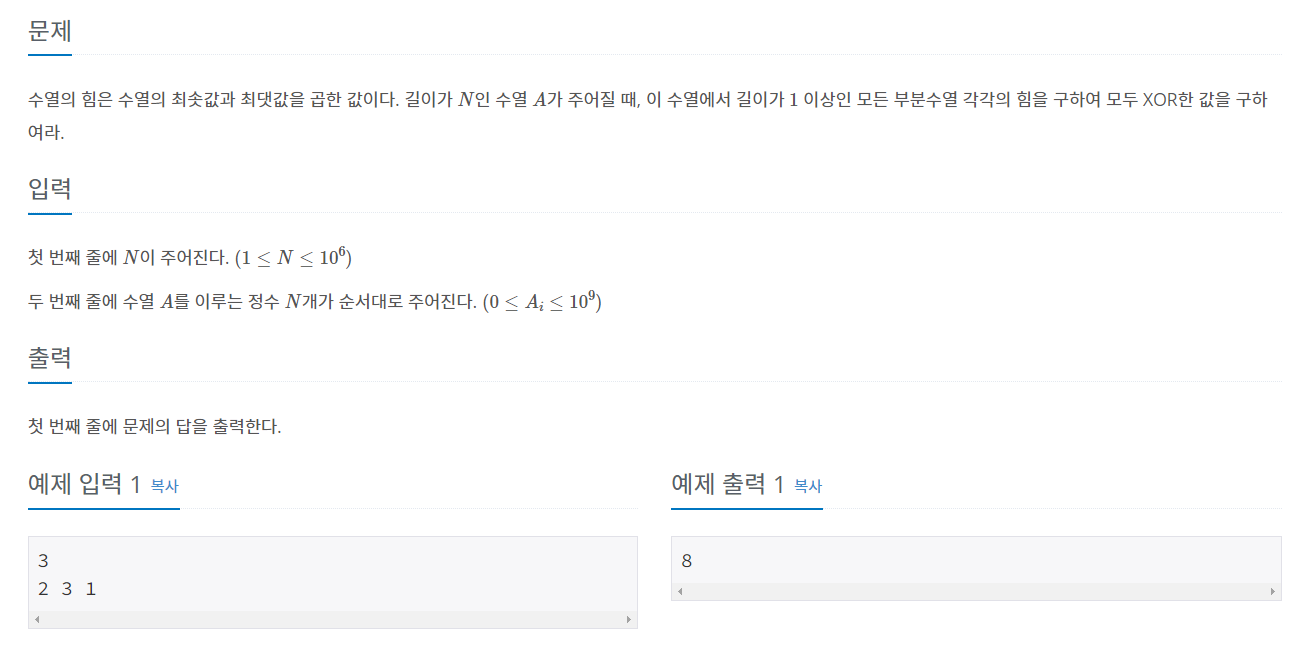
문제의 요구사항은 길이가 "1" 이상인 모든 부분수열 각각의 합을 구하여 모두 XOR한 합을 구하는 것이다. 해당 문제를 보자마자 바로 에드 훅 문제라는것을 생각했지만. 생각보다 푸는데 오랜시간이 소요되었다.
우선 문제를 풀기 위해 XOR 의 특징을 이용하기로 했다. 같은 수 X 를 2^N 번 XOR 연산하면 그 수는 0이 된다.
해당 문제에서 정의하는 부분수열은 인접하지 않아도 되었기 때문에 입력으로 주어진 배열을 오름차순으로 정렬하여 배열을 분석할 수 있다.
2, 3, 1 -> 1, 2, 3
풀이를 좀더 쉽게 생각하기 위해 아래와 같은 배열이 있다고 가정한다
1, 2, 3, 4, 5
최대값의 위치를 M 최소값의 위치를 N 이라 할때 (N < M) 두 수 사이에 있는 숫자의 개수는 M-N-1 개이다
예를들어 1을 최소, 5를 최대로 하는 부분수열이라 가정할때 Zero-based Array 에서 1의 위치는 0, 5의 위치는 4
이므로 1과 5사이에 속한 자연수의 개수는 (2,3,4) 3개이다.
(1) 2 3 4 (5)
여기서 최소 1과 최대 5로 하는 모든 부분수열의 개수는 몇개일까? 바로 2의 3승인 8개이다.
즉 최소와 최대 숫자사이에 K(>=1) 칸 이상 존재할경우 그 수를 XOR 연산하면 결국 0이 된다는 것을 알수있다.
그래서 해당 문제는 결국 정렬했을때의 바로 인접한 두수를 곱하고 계속 XOR 하고, 부분수열의 길이가 1인 경우에는 최소, 최대 모두 K 위치에 있는 값이므로 해당 숫자를 XOR 해주면 풀리는 문제다
(1*2)^(2*3)^(3*4)^(4*5)^(1*1)^(2*2)^(3*3)^(4*4)^(5*5)
코드
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int N;
typedef long long ll;
vector<ll> vec;
int main() {
cin >> N;
for (int i = 0; i < N; i++) {
int num;
cin >> num;
vec.push_back(num);
}
ll ans = 0;
sort(vec.begin(), vec.end());
for (int i = 0; i < vec.size() - 1; i++) {
ans ^= (vec[i] * vec[i + 1]);
}
for (int i = 0; i < N; i++) {
ans ^= vec[i] * vec[i];
}
cout << ans;
return 0;
}'알고리즘 > 백준' 카테고리의 다른 글
| [백준] - PATRIK(3015) (0) | 2023.10.05 |
|---|
